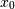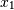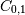常用统计函数

NumPy 提供了很多统计函数，用于从数组中查找最小元素，最大元素，百分位标准差和方差等。

numpy.cumsum()

numpy.cumsum(a, axis=None, dtype=None, out=None)

Parameters:    
    a : array_like
        Input array.

axis : int, optional
    Axis along which the cumulative sum is computed. The default (None) is to compute the cumsum over the flattened array.

    dtype : dtype, optional

按照所给定的轴参数返回元素的梯形累计和，axis=0，按照行累加。axis=1，按照列累加。axis不给定具体值，就把 numpy 数组当成一个一维数组。

>>> a = np.array([[1,2,3], [4,5,6]])
>>> a
array([[1, 2, 3],
       [4, 5, 6]])
>>> np.cumsum(a)
array([ 1,  3,  6, 10, 15, 21])
>>> np.cumsum(a, dtype=float)     # specifies type of output value(s)
array([  1.,   3.,   6.,  10.,  15.,  21.])
>>>
>>> np.cumsum(a,axis=0)      # sum over rows for each of the 3 columns
array([[1, 2, 3],
       [5, 7, 9]])
>>> np.cumsum(a,axis=1)      # sum over columns for each of the 2 rows
array([[ 1,  3,  6],
       [ 4,  9, 15]])

numpy.sum()

numpy.sum(a, axis=None, dtype=None, out=None, 
        keepdims=<no value>, initial=<no value>, where=<no value>)

a：array_like 类型
    待求和的数组。
axis ：可选择None 或int类型 或 整型的tuple类型

>>> np.sum([0.5, 1.5])
2.0
>>> np.sum([0.5, 0.7, 0.2, 1.5], dtype=np.int32)
1
>>> np.sum([[0, 1], [0, 5]])
6
>>> np.sum([[0, 1], [0, 5]], axis=0)
array([0, 6])
>>> np.sum([[0, 1], [0, 5]], axis=1)
array([1, 5])

amin()和 amax()

numpy.amin()用于计算数组中的元素沿指定轴的最小值。

numpy.amax()用于计算数组中的元素沿指定轴的最大值。

import numpy as np

a = np.array([[3, 7, 5], [8, 4, 3], [2, 4, 9]])
print(a)
# [[3 7 5]
#  [8 4 3]
#  [2 4 9]]

print(np.amin(a))
#2

print(np.amin(a, 1))
# 行最小值
# [3 3 2]

print('再次调用 amin() 函数：')
print(np.amin(a, 0))
# 列最小值
# [2 4 3]

print('调用 amax() 函数：')
print(np.amax(a))
# 9

print(np.amax(a, axis=1))
# 行最大值
# [7 8 9]

print('再次调用 amax() 函数：')
print(np.amax(a, axis=0))
# 列最大值
# [8 7 9]

numpy.ptp()

numpy.ptp()函数计算数组中元素最大值与最小值的差（最大值 - 最小值）。

import numpy as np

a = np.array([[3, 7, 5], [8, 4, 3], [2, 4, 9]])
print(a)
# [[3 7 5]
#  [8 4 3]
#  [2 4 9]]
print('调用 ptp() 函数：')
print(np.ptp(a))
# 7

print('沿轴 1 调用 ptp() 函数：')
print(np.ptp(a, axis=1))
# [4 5 7]

print('沿轴 0 调用 ptp() 函数：')
print(np.ptp(a, axis=0))
# [6 3 6]

numpy.median()

计算a在指定轴上的中位数（如果有两个，则取这两个的平均值）

numpy.median(a[, axis, out, overwrite_input, keepdims])

numpy.median() 函数用于计算数组 a 中元素的中位数（中值）

import numpy as np

a = np.array([[30, 65, 70], [80, 95, 10], [50, 90, 60]])
print(a)
# [[30 65 70]
#  [80 95 10]
#  [50 90 60]]
print('调用 median() 函数：')
print(np.median(a))
# 65.0

print('沿轴 0(列) 调用 median() 函数：')
print(np.median(a, axis=0))
# [50. 90. 60.]

print('沿轴 1（行） 调用 median() 函数：')
print(np.median(a, axis=1))
# [65. 80. 60.]

• numpy.nanmedian(a[, axis, out, overwrite_input, ...]) :计算a在指定轴上的中位数，忽略NaN

numpy.mean()

numpy.mean()函数返回数组中元素的算术平均值。 如果提供了轴，则沿其计算。

算术平均值是沿轴的元素的总和除以元素的数量。

import numpy as np

a = np.array([[1, 2, 3], [3, 4, 5], [4, 5, 6]])
print(a)
# [[1 2 3]
#  [3 4 5]
#  [4 5 6]]

print('调用 mean() 函数：')
print(np.mean(a))
#3.6666666666666665

print('沿轴 0 调用 mean() 函数：')
print(np.mean(a, axis=0))
#[2.66666667 3.66666667 4.66666667]

print('沿轴 1 调用 mean() 函数：')
print(np.mean(a, axis=1))
#[2. 4. 5.]

• numpy.nanmean(a[, axis, dtype, out, keepdims]) :计算a在指定轴上的算术均值，忽略NaN

numpy.average()

numpy.average(a[, axis, weights, returned])

numpy.average()函数根据在另一个数组中给出的各自的权重计算数组中元素的加权平均值。

该函数可以接受一个轴参数。 如果没有指定轴，则数组会被展开。

加权平均值即将各数值乘以相应的权数，然后加总求和得到总体值，再除以总的单位数。

考虑数组[1,2,3,4]和相应的权重[4,3,2,1]，通过将相应元素的乘积相加，并将和除以权重的和，来计算加权平均值。

import numpy as np

a = np.array([1, 2, 3, 4])
print(a)
#[1 2 3 4]

print('调用 average() 函数：')
print(np.average(a))
#2.5
# 不指定权重时相当于 mean 函数

wts = np.array([4, 3, 2, 1])
print('再次调用 average() 函数：')
print(np.average(a, weights=wts))
#2.0

# 如果 returned 参数设为 true，则返回权重的和
print('权重的和：')
print(np.average([1, 2, 3, 4], weights=[4, 3, 2, 1], returned=True))
#(2.0, 10.0)
#第二个参数为权重的和

numpy.std()标准差

标准差是一组数据平均值分散程度的一种度量。

标准差是方差的算术平方根。

标准差公式如下：

std = sqrt(mean((x - x.mean())**2))

如果数组是 [1，2，3，4]，则其平均值为 2.5。 因此，差的平方是 [2.25,0.25,0.25,2.25]，并且其平均值的平方根除以 4，即 sqrt(5/4) ，结果为 1.1180339887498949。

import numpy as np 

print (np.std([1,2,3,4]))

1.1180339887498949

• numpy.nanstd(a[, axis, dtype, out, ddof, keepdims]):计算a在指定轴上的标准差，忽略NaN

numpy.var()方差

统计中的方差（样本方差）是每个样本值与全体样本值的平均数之差的平方值的平均数，即 mean((x - x.mean())** 2)。

• 偏样本方差biased sample variance。计算公式为 （ $\bar{x}$为均值）： $v a r=\frac{1}{N} \sum_{i=1}^{N}\left(x_{i}-\bar{x}\right)^{2}$

• 无偏样本方差unbiased sample variance。计算公式为 （ $\bar{x}$为均值）： $v a r=\frac{1}{N-1} \sum_{i=1}^{N}\left(x_{i}-\bar{x}\right)^{2}$ 当ddof=0时，计算偏样本方差；当ddof=1时，计算无偏样本方差。默认值为 0。当ddof为其他整数时，分母就是N-ddof。

换句话说，标准差是方差的平方根。

import numpy as np

print (np.var([1,2,3,4]))

1.25

• numpy.nanvar(a[, axis, dtype, out, ddof, keepdims]) :计算a在指定轴上的方差，忽略 NaN

NumPy 算术函数包含简单的加减乘除: add()，subtract()，multiply()和 divide()。

需要注意的是数组必须具有相同的形状或符合数组广播规则。

numpy.cov()

估计协方差矩阵，给定数据和权重。

numpy.cov(m, y=None, rowvar=True, bias=False, ddof=None, fweights=None, aweights=None)

参数

• m :array_like 包含多个变量和观察值的1-D或2-D数组。M的每一行代表一个变量（即特征），每一列都是对所有这些变量的单一观察（即每一列代表一个样本）

• y :array_like, optional

  另外一组变量和观察结果。 y具有与m相同的形式。

• rowvar : bool,optional

  如果 rowvar 为 True（默认值），则每行代表一个变量，并在列中显示（即每一列为一个样本）。 否则，关系被转置：每列代表变量，而行包含观察值。

• bias : bool,optional

  默认归一化（False）为（N-1），其中N为给定观测次数（无偏估计）。如果bias为True，则归一化为N. 这些值可以通过使用numpy版本> = 1.5中的关键字ddof来覆盖。

• ddof : int,optional

  如果不是，偏移所隐含的默认值将被覆盖。请注意，ddof = 1将返回无偏估计，即使指定了权重和权重，ddof = 0将返回简单平均值。详见附注。 默认值为None。

• fweights :array_like, int, optional

  整数频率权重组成的1-D数组; 代表每个观察向量应重复的次数。

考虑两个变量，和，它们完全相关，但方向相反：

>>> x = np.array([[0, 2], [1, 1], [2, 0]]).T
>>> x
array([[0, 1, 2],
       [2, 1, 0]])

注意增加而减少。协方差矩阵清楚地表明：

>>> np.cov(x)
array([[ 1., -1.],
       [-1.,  1.]])

注意，示出和之间的相关性的元素是负的。

此外，请注意x和y是如何组合的：

>>> x = [-2.1, -1,  4.3]
>>> y = [3,  1.1,  0.12]
>>> X = np.vstack((x,y))
>>> print(np.cov(X))
[[ 11.71        -4.286     ]
 [ -4.286        2.14413333]]
>>> print(np.cov(x, y))
[[ 11.71        -4.286     ]
 [ -4.286        2.14413333]]
>>> print(np.cov(x))
11.71

协方差矩阵计算的是不同维度之间的协方差，而不是不同样本之间。

• numpy.corrcoef(x[, y, rowvar, bias, ddof]) : 返回皮尔逊积差相关
• numpy.correlate(a, v[, mode]) ：返回两个一维数组的互相关系数
• numpy.cov(m[, y, rowvar, bias, ddof, fweights, ...])：返回协方差矩阵

multiply()

import numpy as np 

a = np.arange(9, dtype = np.float_).reshape(3,3)  
print ('第一个数组：')
print (a)
第一个数组：
[[0. 1. 2.]
 [3. 4. 5.]
 [6. 7. 8.]]

print ('第二个数组：')
b = np.array([10,10,10])  
print (b)
第二个数组：
[10 10 10]


print ('两个数组相加：')
print (np.add(a,b))
两个数组相加：
[[10. 11. 12.]
 [13. 14. 15.]
 [16. 17. 18.]]


print ('两个数组相减：')
print (np.subtract(a,b))
两个数组相减：
[[-10.  -9.  -8.]
 [ -7.  -6.  -5.]
 [ -4.  -3.  -2.]]

print ('两个数组相乘：')
print (np.multiply(a,b))
两个数组相乘：
[[ 0. 10. 20.]
 [30. 40. 50.]
 [60. 70. 80.]]


print ('两个数组相除：')
print (np.divide(a,b))
两个数组相除：
[[0.  0.1 0.2]
 [0.3 0.4 0.5]
 [0.6 0.7 0.8]]

numpy.reciprocal()

numpy.reciprocal() 函数返回参数逐元素的倒数。如 1/4 倒数为 4/1。

import numpy as np 

a = np.array([0.25,  1.33,  1,  100])  
print ('我们的数组是：')
print (a)
print ('\n')
print ('调用 reciprocal 函数：')
print (np.reciprocal(a))

我们的数组是：
[  0.25   1.33   1.   100.  ]


调用 reciprocal 函数：
[4.        0.7518797 1.        0.01     ]

numpy.power()

numpy.power()函数将第一个输入数组中的元素作为底数，计算它与第二个输入数组中相应元素的幂。

import numpy as np 

a = np.array([10,100,1000])  
print ('我们的数组是；')
print (a)
print ('\n') 
print ('调用 power 函数：')
print (np.power(a,2))
print ('\n')
print ('第二个数组：')
b = np.array([1,2,3])  
print (b)
print ('\n')
print ('再次调用 power 函数：')
print (np.power(a,b))


我们的数组是；
[  10  100 1000]


调用 power 函数：
[    100   10000 1000000]


第二个数组：
[1 2 3]


再次调用 power 函数：
[        10      10000 1000000000]

numpy.mod()

numpy.mod() 计算输入数组中相应元素的相除后的余数。 函数 numpy.remainder()也产生相同的结果。

import numpy as np

a = np.array([10,20,30]) 
b = np.array([3,5,7])  
print ('第一个数组：')
print (a)
print ('\n')
print ('第二个数组：')
print (b)
print ('\n')
print ('调用 mod() 函数：')
print (np.mod(a,b))

a = np.array([10, 20, 30])
print(a)
print(np.mod(a, 3))
#[1 2 0]

print ('调用 remainder() 函数：')
print (np.remainder(a,b))



第一个数组：
[10 20 30]


第二个数组：
[3 5 7]


调用 mod() 函数：
[1 0 2]


调用 remainder() 函数：
[1 0 2]

参考

统计