NumPy 常用函数
numpy.argpartition
numpy.argpartition(a, kth, axis=-1, kind='introselect', order=None)
在快排算法中,有一个典型 的操作:partition。这个操作指:根据一个数值x,把数组中的元素划分成两半,使得index前面的元素都不大于x,index后面的元素都不小于x。
numpy 中的 argpartition() 函数就是起的这个作用。对于传入的数组a,先用O(n)复杂度求出第 k 大的数字,然后利用这个第 k 大的数字将数组 a 划分成两半。
(第 k 大的数字, 就是排序(从小到大)后的数组,第k个位置的元素,自己理解的)
此函数不对原数组进行操作,它只返回分区之后的下标。一般 numpy 中以 arg 开头的函数都是返回下标而不改变原数组。
此函数还有另外两个参数:
kind:用于指定partition的算法order:表示排序的key,也就是按哪些字段进行排序
当我们只关心 TopK 时,我们不需要使用np.sort()对数组进行全量排序,np.argpartition()已经够用了。
$ import numpy as np
$ a = np.array([9, 4, 4, 3, 3, 9, 0, 4, 6, 0])
$ print(np.argpartition(a, 4))
#将数组a中所有元素(包括重复元素)从小到大排列,比第5大的元素小的放在前面,大的放在后面,输出新数组索引
>> [6 9 4 3 7 2 1 5 8 0]
$ a[np.argpartition(a, 4)] #输出新数组索引对应的数组
>> array([0, 0, 3, 3, 4, 4, 4, 9, 6, 9])
注意,排序规则是从0开始排序,即,第0大的元素为“0”,第1大的元素还为“0”,第2大的元素为“3”
>>> arr = np.array([8,7,6,5,4,3,2,1])
>>> np.argpartition(arr, 0)
array([7, 1, 2, 3, 4, 5, 6, 0], dtype=int32)
>>> np.argpartition(arr, 1)
array([7, 6, 2, 3, 4, 5, 1, 0], dtype=int32)
>>> np.argpartition(arr, 2)
array([7, 6, 5, 3, 4, 2, 1, 0], dtype=int32)
>>> np.argpartition(arr, 3)
array([6, 7, 5, 4, 3, 1, 2, 0], dtype=int32)
>>> np.argpartition(arr, 4)
array([4, 7, 6, 5, 3, 1, 2, 0], dtype=int32)
>>> np.argpartition(arr, 5)
array([4, 7, 6, 5, 3, 2, 1, 0], dtype=int32)
>>> np.argpartition(arr, 6)
array([4, 7, 6, 5, 3, 2, 1, 0], dtype=int32)
>>> np.argpartition(arr, 7)
array([4, 7, 6, 5, 3, 2, 1, 0], dtype=int32)
第一次调用,给第二个参数传了0,说明我需要返回最小值得索引index。得到的返回值是array([7, 1, 2, 3, 4, 5, 6, 0], dtype=int32),在这个返回的array中,我关心的是第0个值(7),它是原数组arr的索引,arr[7]就是我要找的最小值。请注意返回值中的其他几个索引值,和原数组的索引比起来,他们基本上没有什么变化。接下来的几次调用也是这种情况,其实这也就说明argpartition没有对他不关心的数据做太大的改动或者操作。
$ import numpy as np
$ a = np.array([9, 4, 4, 3, 3, 9, 0, 4, 6, 0])
$ a[np.argpartition(a, -5)[-5:]]
>> array([4, 4, 9, 6, 9])
numpy.clip
numpy.clip(a, a_min, a_max, out=None)[source]
在很多数据处理和算法中(比如强化学习中的 PPO),我们需要使得所有的值保持在一个上下限区间内。Numpy 内置的 Clip 函数可以解决这个问题。Numpy clip () 函数用于对数组中的值进行限制。给定一个区间范围,区间范围外的值将被截断到区间的边界上。例如,如果指定的区间是 [-1,1],小于-1 的值将变为-1,而大于 1 的值将变为 1

Clip示例:限制数组中的最小值为 2,最大值为 6。
array = np.array([10, 7, 4, 3, 2, 2, 5, 9, 0, 4, 6, 0])
np.clip(array,2,5)
# array([5, 5, 4, 3, 2, 2, 5, 5, 2, 4, 5, 2])
array = np.array([10, -1, 4, -3, 2, 7, 5, 9, 0, 4, 6, 0])
# array([6, 2, 4, 2, 2, 2, 5, 6, 2, 4, 6, 2])
高维数组也是一样的
x=np.array([[1,2,3,5,6,7,8,9],[1,2,3,5,6,7,8,9]])
np.clip(x,3,8)
Out[90]:
array([[3, 3, 3, 5, 6, 7, 8, 8],
[3, 3, 3, 5, 6, 7, 8, 8]])
numpy.where()
numpy.where()函数,此函数返回数组中满足某个条件的元素的索引
np.where(condition, x, y)
三目运算满足condition,为x;不满足condition,则为y
score = np.array([[80, 88], [82, 81], [84, 75], [86, 83], [75, 81]])
# 如果数值小于80,替换为0,如果大于等于80,替换为90
re_score = np.where(score < 80, 0, 90)
print(re_score)
shuchu:
[[90 90]
[90 90]
[90 0]
[90 90]
[ 0 90]]
np.where(condition)
只有条件 (condition),没有x和y,则输出满足条件 (即非0) 元素的坐标 (等价于numpy.nonzero)。这里的坐标以tuple的形式给出,通常原数组有多少维,输出的tuple中就包含几个数组,分别对应符合条件元素的各维坐标。
//这里我们输出x数据中大于5的元素的索引
y=np.where(x>5)
print(y)
输出结果:
(array([1, 2, 2, 2], dtype=int64), array([2, 0, 1, 2], dtype=int64))
//使用索引取出元素"
print(x[y])
输出结果:
[6 7 8 9]
numpy.extract()
从数组中提取符合条件的元素
numpy.extract()函数,和where函数有一点相,不过extract函数是返回满足条件的元素,而不是元素索引
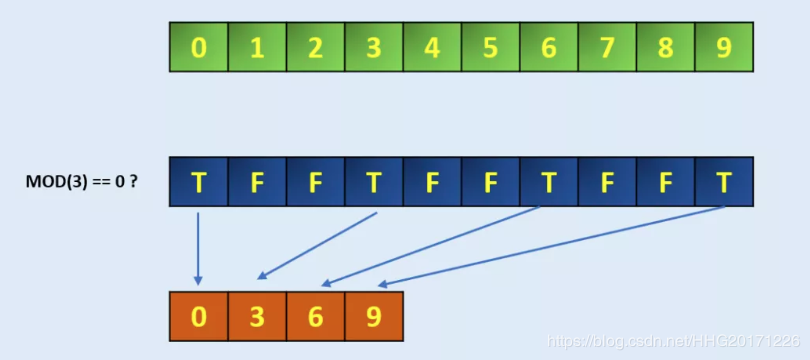
arr = np.arange(10)
arrarray([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])# Define the codition, here we take MOD 3 if zero
condition = np.mod(arr, 3)==0
#conditionarray([ True, False, False, True, False, False, True, False, False,True])
np.extract(condition, arr)
#array([0, 3, 6, 9])
同样地,如果有需要,我们可以用 AND 和 OR 组合的直接条件,如下所示:
np.extract(((arr > 2) & (arr < 8)), arr)
#array([3, 4, 5, 6, 7])
#定义条件,(元素 % 2==0)
condition=np.mod(x,2)==0
print(condition)
输出结果:
[[False True False]
[ True False True]
[False True False]]
返回满足条件的元素:
//获取满足条件的元素
print(np.extract(condition,x))
输出结果:
[2 4 6 8]
numpy.setdiff1d
如何找到仅在 A 数组中有而 B 数组没有的元素
setdiff1d(ar1, ar2, assume_unique=False)
1.功能:找到2个数组中集合元素的差异。
2.返回值:在ar1中但不在ar2中的'已排序'的'唯一值'。
3.参数:
ar1:array_like 输入数组。
ar2:array_like 输入比较数组。
assume_unique:bool。如果为True,则假定输入数组是唯一的,即可以加快计算速度。 默认值为False。
返回数组中不在另一个数组中的独有元素。这等价于两个数组元素集合的差集。
a = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9])
b = np.array([3,4,7,6,7,8,11,12,14])
c = np.setdiff1d(a,b)
carray([1, 2, 5, 9])
numpy.intersect1d()
求两个数组的交集
>>> np.intersect1d([1, 3, 4, 3], [3, 1, 2, 1])
array([1, 3])
要求交集的数组多于两个, 可使用functools.reduce:
>>> from functools import reduce
>>> reduce(np.intersect1d, ([1, 3, 4, 3], [3, 1, 2, 1], [6, 3, 4, 2]))
array([3])
numpy.nonzero()
numpy.nonzero(a)
返回数组 a 中非零元素的索引值数组。
(1)只有 a 中非零元素才会有索引值,那些零值元素没有索引值;
(2)返回的索引值数组是一个2维 tuple 数组,该 tuple 数组中包含一维的array数组。其中,一维 array 向量的个数与 a 的维数是一致的。
(3)索引值数组的每一个array均是从一个维度上来描述其索引值。比如,如果a是一个二维数组,则索引值数组有两个 array,第一个 array 从行维度来描述索引值;第二个 array 从列维度来描述索引值。
(4) 该np.transpose(np.nonzero(x))
函数能够描述出每一个非零元素在不同维度的索引值。
(5)通过 a[nonzero(a)]得到所有a中的非零值
nz = np.nonzero([1,2,0,0,4,0])
nz
#(array([0, 1, 4], dtype=int64),)
nz[0]
#array([0, 1, 4], dtype=int64)
nz[0]
#array([0, 1, 4], dtype=int64)
numpy.pad()
np.pad(array,pad_width,mode,**kwars)
解释:
第一个参数是待填充数组
第二个参数是填充的形状,(2,3)表示前面两个,后面三个
第三个参数是填充的方法
填充方法:
constant连续一样的值填充,有关于其填充值的参数。
constant_values=(x, y)时前面用x填充,后面用y填充。缺参数是为0000。。。
edge用边缘值填充
linear_ramp边缘递减的填充方式
maximum, mean, median, minimum分别用最大值、均值、中位数和最小值填充
reflect, symmetric都是对称填充。前一个是关于边缘对称,后一个是关于边缘外的空气对称╮(╯▽╰)╭
wrap用原数组后面的值填充前面,前面的值填充后面
也可以有其他自定义的填充方法
numpy.percentile()
分位数函数
在 python 中计算一个多维数组的任意百分比分位数,此处的百分位是从小到大排列,只需用np.percentile即可……
numpy.percentile(a, q, axis=None, out=None, overwrite_input=False, interpolation='linear', keepdims=False)
a : np数组
q : float in range of [0,100] (or sequence of floats)
Percentile to compute。
要计算的q分位数。
axis : 那个轴上运算。
keepdims :bool是否保持维度不变。
import numpy as np
a = np.array([1,2,3,4,5])
p = np.percentile(a, 50) # 求中位数
# 3
>>> a = np.array([[10, 7, 4], [3, 2, 1]])
>>> a
array([[10, 7, 4],
[ 3, 2, 1]])
>>> np.percentile(a, 50) #50%的分位数,就是a里排序之后的中位数
3.5
>>> np.percentile(a, 50, axis=0) #axis为0,在纵列上求
array([[ 6.5, 4.5, 2.5]])
>>> np.percentile(a, 50, axis=1) #axis为1,在横行上求
array([ 7., 2.])
>>> np.percentile(a, 50, axis=1, keepdims=True) #keepdims=True保持维度不变
array([[ 7.],
[ 2.]])
numpy.nanpercentile
忽略空值的百分位数
numpy.count_nonzero()
numpy.count_nonzero(a)
计算数组a中非零值的数量。
>>> np.count_nonzero(np.eye(4))
4
>>> np.count_nonzero([[0,1,7,0,0],[3,0,0,2,19]])
5
numpy.nonzero()
返回非零元素的索引。
返回数组的元组,每个维度a一个,包含该维度中非零元素的索引。a中的值总是以行主,C风格顺序测试和返回。相应的非零值可以用下式获得:
>>> x
array([[ 1., 0., 0.],
[ 0., 1., 0.],
[ 0., 0., 1.]])
>>> np.nonzero(x)
(array([0, 1, 2]), array([0, 1, 2]))
>>> x[np.nonzero(x)]
array([ 1., 1., 1.])
>>> np.transpose(np.nonzero(x))
array([[0, 0],
[1, 1],
[2, 2]])
nonzero的常见用法是找到数组的索引,其中条件为True。
>>> a = np.array([[1,2,3],[4,5,6],[7,8,9]])
>>> a > 3
array([[False, False, False],
[ True, True, True],
[ True, True, True]], dtype=bool)
>>> np.nonzero(a > 3)
(array([1, 1, 1, 2, 2, 2]), array([0, 1, 2, 0, 1, 2]))